ヒープ
ヒープ (Heap) は「ヒープ特性」を満たす特殊な木構造です。
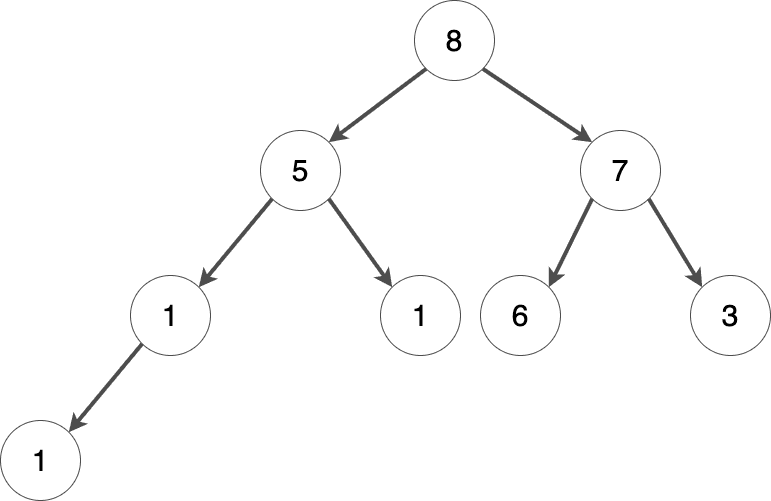
ヒープには主に2つの種類があります:
最大ヒープ (Max Heap): 親ノードの値が子ノードの値よりも大きい(または等しい)必要があります。
最小ヒープ (Min Heap): 親ノードの値が子ノードの値よりも小さい(または等しい)必要があります。
優先度付きキューの多くは最大ヒープを内部実装として利用しているため、ここでは最大ヒープに注目します。最大ヒープにおいては、根ノードが最も大きな要素となり、葉ノードが最も小さくなります。ただし、葉同士の間には特に順序はありません。保証されるのは、根ノードが最も大きく、その子ノードは根ノード以下の値であるという点だけです。
また、ヒープの最下段の要素は常に左から右の順で埋められます。つまり、左側の葉から順番に位置が決まっていき、最後に右側の葉が埋まる形となります。上の図がその例を示しています。
実装
ヒープは配列で実装できます。配列の先頭要素が根ノードを表します。ノードには子ノードが2つずつしかないため、次のようにインデックスを割り当てられます:
根ノードのインデックスは 1 とする。
すべてのノードについて、左の子と右の子はそれぞれ
2iおよび2i+1に位置する。インデックス
iの要素の親ノードはi // 2に位置する。
上のヒープは、次のようにリストで表すことができます:
# 画像の各行を順番に読み取り、数字を横に並べるだけです
heap = [None, 8, 5, 7, 1, 1, 6, 3, 1]
# もしくは、より見やすくするために
heap = [None, # インデックスを簡単にするため、[0] は使いません
8, # インデックス [1]
5, 7, # インデックス [2, 3]
1, 1, 6, 3, # インデックス [4, 5, 6, 7]
1] # インデックス [8]チャレンジ: 二分木がヒープかどうかをチェックする
配列で表された n 個の数値による二分木(先述のインデックス割り当てに従ったもの)が与えられたとき、最大ヒープの特性を満たしているかどうかを判定してください。
入力
最初の行には整数 n (1 ≤ n ≤ 100 000) が与えられます。
次の行には n 個の整数 () が空白区切りで与えられ、それぞれがヒープの要素の値を表します。
出力
入力として与えられる二分木が最大ヒープの特性を満たす場合は Yes、満たさない場合は No を出力してください。
例
Input | Output |
|---|---|
8 | Yes |
7 | No |
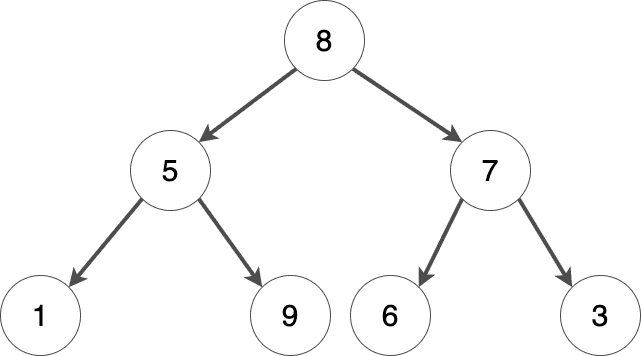
解説
例 1

例 2
Constraints
Time limit: 1.6 seconds
Memory limit: 512 MB
Output limit: 1 MB