二分木の表現
二分木は、コンピューターサイエンスで広く使われている基本的なデータ構造です。探索やソート、データの走査などの処理を効率よく行うアルゴリズムを構築する上で、特に有用です。
二分木はノードから構成され、それぞれのノードは最大で2つの子ノード(左の子と右の子)を持ちます。左と右の子ノードも同様に、さらに左と右の子ノードを持つ可能性があり、これ以上ノードがないところまでその構造が続きます。
木の最上部にあるノードはルート(根)と呼ばれ、一番下にあるノードは葉(リーフ)と呼ばれます。
このシンプルな仕組みによって、驚くほどさまざまなデータを効率的に表現でき、複数のプログラミング言語で容易に実装できます:
class Node: # 各ノードのデータを保持するためのNodeオブジェクト
def __init__(self, value): # 各ノードに保持する値(内容は何でも可)
self.left = None # 最初はleftとrightの両方がNone
self.right = None
self.value = value # 値をオブジェクトとして保持する
# すべてのノードを手動で作成
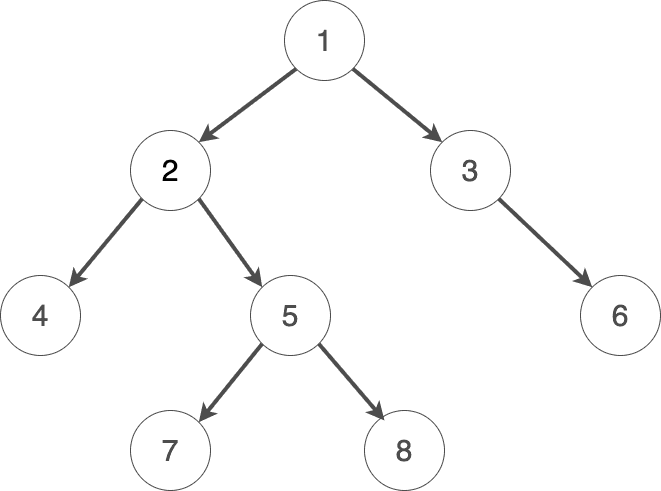
root = Node(1)
root.left, root.right = Node(2), Node(3)
root.left.left, root.left.right = Node(4), Node(5)
root.left.right.left, root.left.right.right = Node(7), Node(8)
root.right.right = Node(6)
# ここからバイナリツリー全体を再帰的に走査できる
# すべてのノードの合計値を計算してみる
def treesum(node: Node | None) -> int:
if node is None:
return 0
# 左部分木、右部分木、そして現在のノードの値を合計して返す
return treesum(node.left) + treesum(node.right) + node.value
print(treesum(root)) # 36を出力この例では、root から始めてすべてのノードを走査します。現在のノードが None であれば、そのパス上の部分木が終わったことを意味するため、合計として 0 を返します。そうでなければ、左部分木、右部分木、そして現在のノードの値を足し合わせ、その合計を返す仕組みになっています。
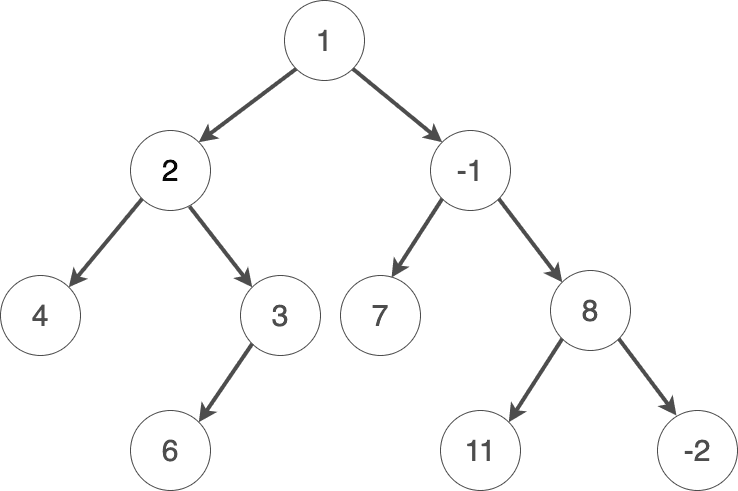
チャレンジ: 二分木を手動で作成
図に示されている二分木を、手動で作成するコードを書いてみてください。出力をする必要はありません。表示の部分は自動的に行われます。
Constraints
Time limit: 1.6 seconds
Memory limit: 512 MB
Output limit: 1 MB