ヒープを整形する (Heapify the Heap)
ヒープで行える主な操作は2つあり、要素の追加とルートノードの削除が挙げられます。
これらの操作を行うたびに、ヒープの性質が損なわれないように気をつける必要があります。
ルートを削除するときには、ルートから最下層まで順に構造を修正し、すべての親ノードの値が子ノードの値よりも大きくなる(最大ヒープの場合)ように調整します。
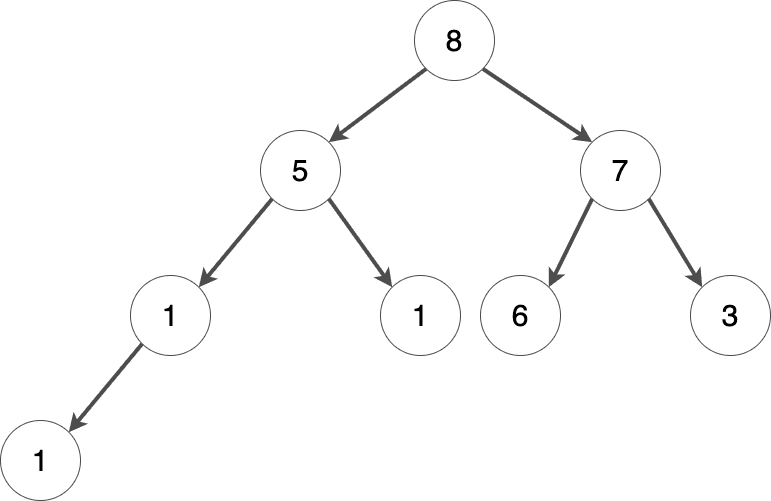
要素を追加する際には、逆に最下層からルートノードに向かって構造を修正し、親ノードの値が子ノードより常に大きい状態を保ちます。
Insert a New Element Into a Heap
新しい値を挿入するには、まず配列の末尾に値を追加し、続いて、その新しく挿入した値と親ノードを比較しながら必要に応じて入れ替える操作を繰り返し、ヒープの性質を回復させます:
heap = [None, 8, 5, 7, 1, 1, 6, 3, 1] # 初期ヒープ
heap.append(6) # 値6の新しい要素を追加
# 浮かし上げ処理でヒープの性質を修正
node = len(heap) - 1 # 現在のノードのインデックス
while node > 1: # ルートに到達するまで
parent = node // 2 # 親ノードのインデックスを取得
if heap[node] > heap[parent]: # ヒープ構造が正しくない場合
heap[node], heap[parent] = heap[parent], heap[node]
else: # 構造が正しければ
break # それより上も正しいので終了
node //= 2 # 親ノードへ移動Delete the Root Element of a Heap
ルート要素を削除するには、まず配列の最後の要素をルート位置と入れ替え、そこからヒープの性質が復元できるように繰り返しノードとより大きい子ノード(最大ヒープの場合)を入れ替えていきます:
heap = [None, 8, 5, 7, 1, 1, 6, 3, 1] # 初期ヒープ
heap[1], heap[-1] = heap[-1], heap[1] # ルートと末尾の要素を入れ替える
heap.pop() # 末尾の要素(元ルート)を削除
# 下りながらヒープの性質を修正
node = 1 # 現在のノードのインデックス
while node < len(heap): # 範囲を超えるまで
left = heap[2 * node] if 2 * node < len(heap) else float('-inf')
right = heap[2 * node + 1] if 2 * node + 1 < len(heap) else float('-inf')
# ヒープの性質が満たされていれば終了
if heap[node] >= left and heap[node] >= right:
break
# left > right の場合は左の子へ移動
if left > right:
heap[2 * node], heap[node] = heap[node], heap[2 * node]
node = 2 * node
else:
heap[2 * node + 1], heap[node] = heap[node], heap[2 * node + 1]
node = 2 * node + 1Challenge: Fix the Heap
与えられた 最小ヒープ(min-heap) には n 個の数があり、n-1 個の要素はすでに最小ヒープの性質を満たしています。しかし n 番目の要素が性質を損ねている可能性があります。このとき、すべての要素が最小ヒープの性質を満たすように修正してください。
Input
入力の最初の行には整数 n (1 ≤ n ≤ ) が1つ与えられます。
次の行には、ヒープを構成する n 個の整数 () が空白区切りで与えられます。
Output
修正後のヒープを表す n 個の整数を空白区切りで出力してください。
Examples
入力 | 出力 |
|---|---|
7 | -3 2 1 4 3 6 5 |
6 | 5 6 8 20 10 9 |
Explanation
Example 1
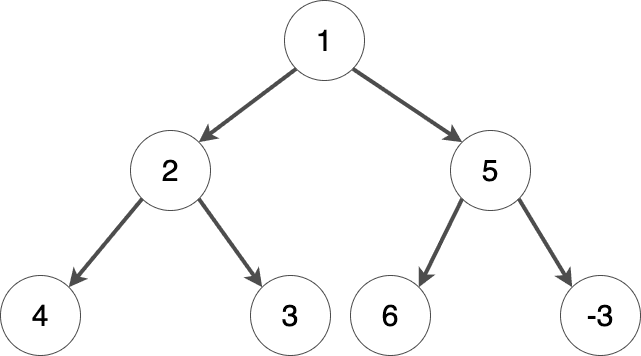
Example 2
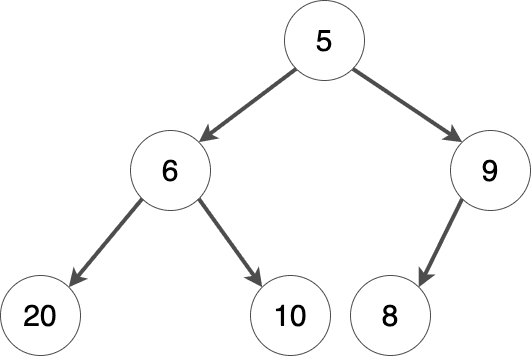
Constraints
Time limit: 4 seconds
Memory limit: 512 MB
Output limit: 10 MB