隣接行列 (Adjacency Matrix) – グラフの表現
グラフとは、頂点（ノード）とそれらを結ぶ辺から構成される構造のことです。グラフは、物体同士の関係性を表現したり、ネットワークを表すために利用できます。都市や人、あるいはもっと抽象的な要素のつながりを表す際によく使われる手法です。
グラフには、有向グラフと無向グラフの2種類があります:
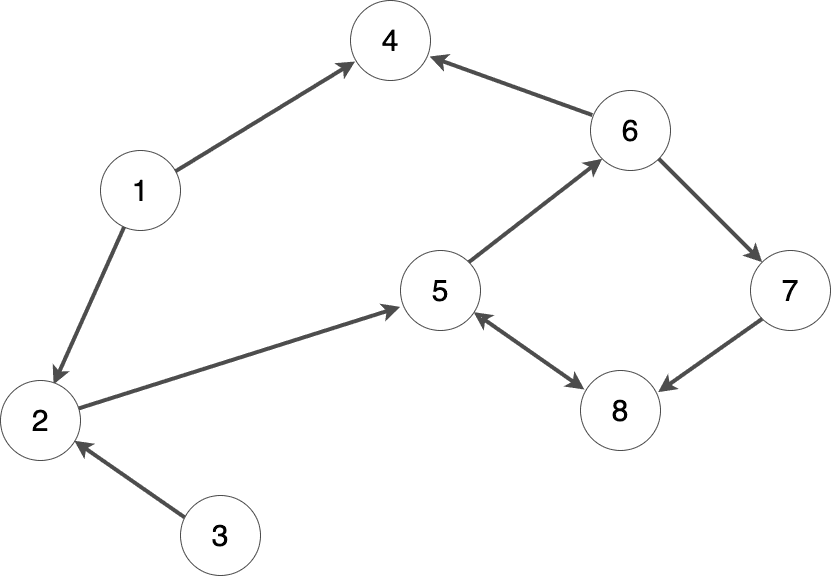
- Directed graphs (有向グラフ): すべての辺に向きがあり、一方の頂点から別の頂点へ「道」があっても、逆方向にはない場合があります。いわゆる一方通行の道路のようなイメージです。
Yet, it’s possible to have both directions in a directed graph. They are just explicitly marked for that (the connection between vertices 5 and 8 in the graph).
- Undirected graphs (無向グラフ): 辺に向きがなく、もし2つの頂点の間に辺があれば、その頂点同士は両方向でつながっています。
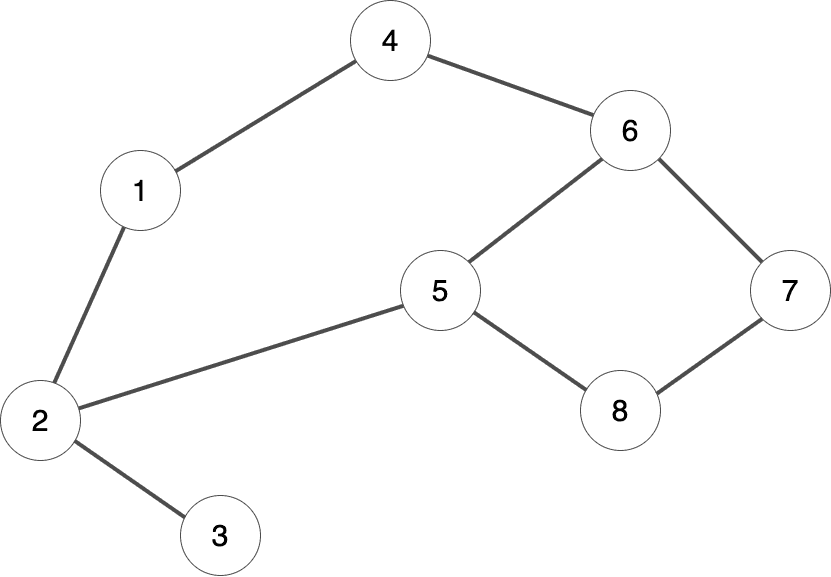
グラフを表現する方法の一つに「隣接行列 (Adjacency Matrix)」があります。これはグラフ全体を表す正方行列で、行と列がそれぞれグラフの頂点を表します。もし2つの頂点の間に辺があれば、該当する行と列のセルが1になり、辺がなければ0になります。
先ほどの有向グラフを隣接行列で表すと、次のような例が考えられます:
g = [
# 1 2 3 4 5 6 7 8
[0, 1, 0, 1, 0, 0, 0, 0], # 頂点1から出る接続
[0, 0, 0, 0, 1, 0, 0, 0], # 頂点2から出る接続
[0, 1, 0, 0, 0, 0, 0, 0], # 頂点3から出る接続
[0, 0, 0, 0, 0, 0, 0, 0], # 頂点4から出る接続
[0, 0, 0, 0, 0, 1, 0, 1], # 頂点5から出る接続
[0, 0, 0, 1, 0, 0, 1, 0], # 頂点6から出る接続
[0, 0, 0, 0, 0, 0, 0, 1], # 頂点7から出る接続
[0, 0, 0, 0, 1, 0, 0, 0], # 頂点8から出る接続
]双方向の辺がある場合は、両頂点に対して1が入るのが特徴です。
また、ここでは頂点の番号と行列のインデックスをずらして使っています。そのため、たとえば
g[0] にアクセスすると、実際には「頂点1」の接続先を参照することになります。画像で示した番号と行列 g のインデックスを1対1で対応させたい場合は、9行×9列にしても問題ありません。どちらを使うかはお好みです 😎。チャレンジ: Edges to Adjacency Matrix
「v 個の頂点」と「e 本の辺」をもつグラフが与えられたとき、そのグラフの隣接行列を作成してください。
入力 (Input)
最初の行に
v (1 ≤ v ≤ 1000) と e (1 ≤ e ≤ 100 000) が与えられます。続く
e 行では、v1 と v2 (1 ≤ v1, v2 ≤ v) のペアが与えられ、これは頂点 v1 と頂点 v2 が互いに接続していることを表します。出力 (Output)
与えられたグラフの隣接行列を出力してください。各行の要素はスペース区切りで表示します。
例 (Examples)
入力 (Input) | 出力 (Output) |
8 9
1 4
4 6
3 2
2 1
5 2
5 6
8 5
7 6
7 8 | 0 1 0 1 0 0 0 0
1 0 1 0 1 0 0 0
0 1 0 0 0 0 0 0
1 0 0 0 0 1 0 0
0 1 0 0 0 1 0 1
0 0 0 1 1 0 1 0
0 0 0 0 0 1 0 1
0 0 0 0 1 0 1 0 |
Constraints
Time limit: 2 seconds
Memory limit: 512 MB
Output limit: 5 MB