隣接リスト - グラフの表現
グラフを表現する方法としては、隣接リスト（Adjacency List）が非常に広く使われています。隣接リストはリストの配列としてグラフを表現する方法で、配列の各要素はグラフの頂点に対応し、その頂点に隣接する頂点のリストを保持します。
与えられた有向グラフの例から、以下のように隣接リストを作成できます:
g = [
[], # 頂点0はスキップ
[2, 4], # 頂点1
[5], # 頂点2
[2], # 頂点3
[], # 頂点4
[6, 8], # 頂点5
[4, 7], # 頂点6
[8], # 頂点7
[5], # 頂点8
]
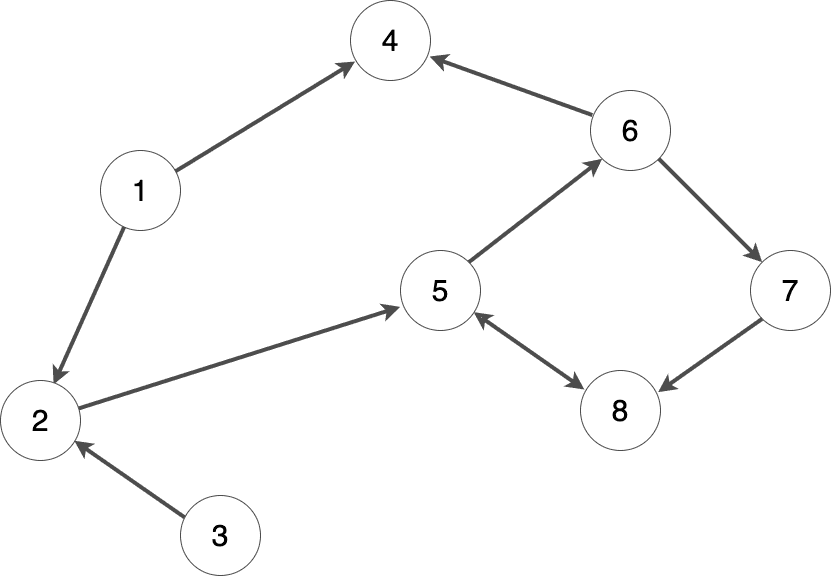
ご覧のとおり、辺の数がそれほど多くないグラフでは、隣接行列よりも隣接リストを用いた表現のほうがずっとコンパクトになります。ただし、グラフの辺が非常に多い場合は、隣接行列で表現したほうが効率的になることもあります。
チャレンジ: Edges to Adjacency List
無向グラフで頂点数が
v、辺の数が e のとき、その隣接リストを作成してください。入力
最初の行に、頂点数
v (1 ≤ v ≤ 100 000) と辺の数 e (1 ≤ e ≤ 100 000) が与えられます。続く
e 行では、2 つの整数 v1, v2 (1 ≤ v1, v2 ≤ v) が与えられます。これは頂点 v1 と頂点 v2 が互いに接続されていることを意味します。出力
与えられたグラフの隣接リストを出力してください。各行は、頂点の番号とコロン (
:) の後に、その頂点に隣接する頂点の一覧を空白で区切って出力します。頂点や隣接頂点の並び順については特に指定はありません。例
入力 | 出力 |
8 9
1 4
4 6
3 2
2 1
5 2
5 6
8 5
7 6
7 8 | 1: 2 4
2: 1 3 5
3: 2
4: 1 6
5: 2 6 8
6: 4 7 5
7: 8 6
8: 5 7 |
解説
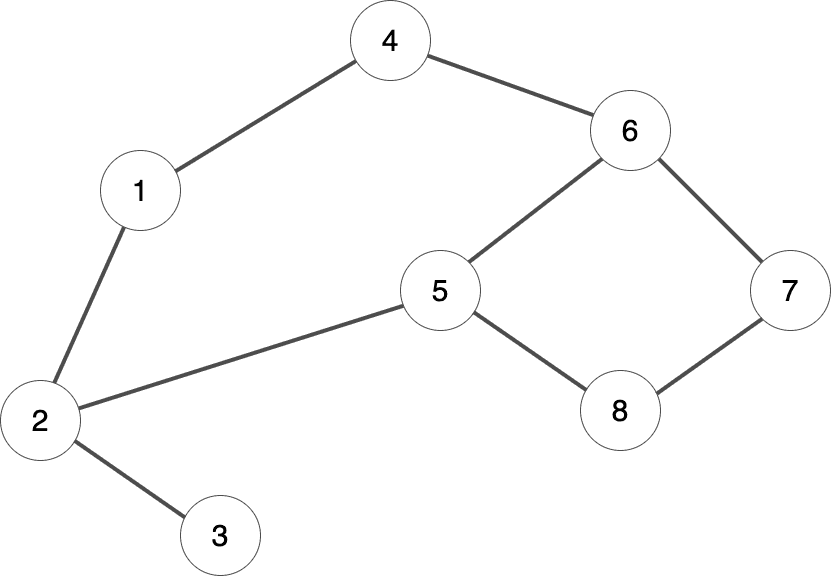
Constraints
Time limit: 2.2 seconds
Memory limit: 512 MB
Output limit: 1 MB