Find the Isolated Vertices in a Graph
A vertex in a graph is considered isolated if it does not have any edges.
Given an undirected graph with v vertices and e edges, you are asked to determine for each vertex if it’s isolated.
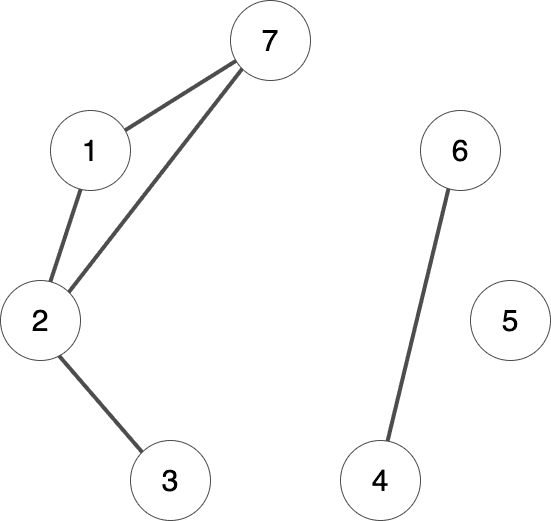
Vertex 5, for instance, in the image is an isolated vertex, while all the other vertices are not as they have neighbors.
Input
The first line of the input contains two integers v (1 ≤ v ≤ 100 000) and e (1 ≤ e ≤ 100 000).
The following e lines contain pairs of integers v1, v2 (1 ≤ v1, v2 ≤ v) which means that the vertex v1 is connected to the vertex v2 and vice versa.
Output
The program should v lines each one being Yes if the corresponding vertex is isolated and No otherwise. The vertices are numbered from 1 to v.
Examples
Input | Output |
|---|---|
3 2 | No |
7 5 | No |
Constraints
Time limit: 1.6 seconds
Memory limit: 512 MB
Output limit: 1 MB